潜在狄利克雷分配（latent Dirichlet allocation, LDA）

$$\begin{align} \end{align}$$

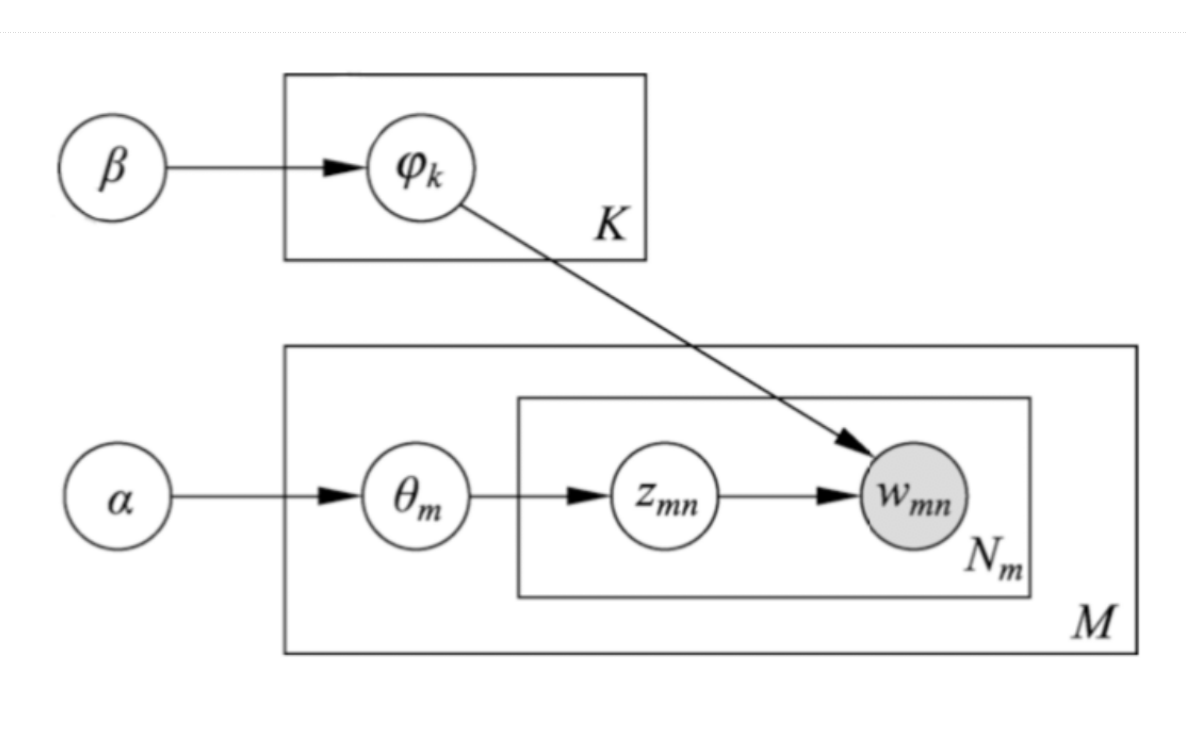
潜在狄利克雷分配模型定义：

单词集合

$$W=\left\{w_1,w_2,\cdots,w_v,\cdots,w_V\right\}$$

其中，$w_v$是第$v$个单词，$v=1,2,\cdots,V$，$V$是单词的个数。

文本集合

$$D=\left\{\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_m,\cdots,\mathbf{w}_M\right\}$$

其中，$\mathbf{w}_m$是第$m$个文本，$m=1,2,\cdots,M$，$M$是文本个数。
文本$\mathbf{w}_m=\left(w_{m1},w_{m2},\cdots,w_{mn},\cdots,w_{mN_m}\right)$是一个单词序列，其中$w_{mn}$是文本$\mathbf{w}_m$的第$n$个单词，$n=1,2,\cdots,N_m$，$N_m$是文本$\mathbf{w}_m$中的单词个数。

话题集合

$$Z=\left\{z_1,z_2,\cdots,z_k,\cdots,z_K\right\}$$

其中，$z_k$是第$k$个话题，$k=1,2,\cdots,K$，$K$是话题个数。

每一个话题$z_k$包含的单词由条件概率分布$p\left(w|z_k\right)$决定，$w\in W$。分布$p\left(w|z_k\right)$服从多项分布，其参数为$\varphi_k=\left(\varphi_{k1},\varphi_{k2},\cdots,\varphi_{kV}\right)$是一个$V$维向量，$\varphi_{kv}$表示话题$z_k$生成单词$w_v$的概率。所有话题的参数向量构成一个$K\times V$矩阵，$\boldsymbol{\varphi}=\left\{\varphi_k\right\}_{k=1}^K$。参数$\varphi_k$服从狄利克雷分布，其超参数$\beta=\left(\beta_1,\beta_2,\cdots,\beta_V\right)$也是一个$V$维向量。

每一个文本$\mathbf{w}_m$包含的话题由条件概率分布$p\left(z|\mathbf{w}_m\right)$决定，$z\in Z$。分布$p\left(z|\mathbf{w}_m\right)$服从多项分布，其参数为$\theta_m=\left(\theta_{m1},\theta_{m2},\cdots,\theta_{mK}\right)$是一个$K$维向量，$\theta_{mk}$表示文本$\mathbf{w}_m$生成话题$z_k$的概率。所有文本的参数向量构成一个$M\times K$矩阵，$\boldsymbol{\theta}=\left\{\theta_m\right\}_{m=1}^M$。参数$\theta_m$服从狄利克雷分布，其超参数$\alpha=\left(\alpha_1,\alpha2,\cdots,\alpha_K\right)$也是一个$K$维向量。

潜在狄利克雷分配文本集合的生成过程：
给定单词集合$W$，文本集合$D$，话题集合$Z$，狄利克雷分布的参数$\alpha$和$\beta$。

1. 生成话题的单词分布
   随机生成$K$个话题的单词分布。按照狄利克雷分布$Dir\left(\beta\right)$随机生成一个参数向量$\varphi_k$，$\varphi_k\thicksim Dir\left(\beta\right)$，作为话题$z_k$的单词分布$p\left(w|z_k\right),w\in W,k=1,2,\cdots,K$。
2. 生成文本的话题分布
   随机生成$M$个文本的话题分布。按照狄利克雷分布$Dir\left(\alpha\right)$随机生成一个参数向量$\theta_m$，$\theta_m\thicksim Dir\left(\alpha\right)$，作为文本$\mathbf{w}_m$的话题分布$p\left(z|\mathbf{w}_m\right),z\in Z,m=1,2,\cdots,M$。
3. 生成文本的单词序列
   随机生成$M$个文本的$N_m$个单词。文本$\mathbf{w}_m\left(m=1,2,\cdots,M\right)$的单词$w_{mn}\left(n=1,2,\cdots,N_m\right)$的生成过程：
   a. 按照多项分布$Mult\left(\theta_m\right)$随机生成一个话题$z_{mn},z_{mn}\thicksim Mult\left(\theta_m\right)$。
   b. 按照多项分布$Mult\left(\varphi_{z_{mn}}\right)$随机生成一个单词$w_{mn},w_{mn}\thicksim Mult\left(\varphi_{z_{mn}}\right)$。

文本$\mathbf{w}_m$本身是单词序列$\mathbf{w}_m=\left(w_{m1},w_{m2},\cdots,w_{mN_m}\right)$，对应隐式的话题序列$\mathbf{z}_m=\left(z_{m1},z_{m2},\cdots,z_{mN_m}\right)$。

LDA文本生成算法：
输入：单词集合$W$，话题集合$Z$，狄利克雷函数分布的参数$\alpha$和$\beta$；
输出：文本集合$D$;

1. 对于话题$z_k\left(k=1,2,\cdots,K\right)$:
   生成多项分布参数$\varphi_k\thicksim Dir\left(\beta\right)$，作为话题的单词分布$p\left(w|z_k\right)$;
2. 对于文本$\mathbf{w}_m\left(m=1,2,\cdots,M\right)$:
   生成所想分布参数$\theta_m\thicksim Dir\left(\alpha\right)$，作为文本的话题分布$p\left(z|\mathbf{w}_m\right)$;
3. 对于文本$\mathbf{w}_m$的单词$w_{mn}\left(m=1,2,\cdots,M;n=1,2,\cdots,N_m\right)$:
   a. 生成话题$z_{mn}\thicksim Mult\left(\theta_m\right)$，作为单词对应的话题；
   b. 生成单词$w_{mn}\thicksim Mult\left(\varphi_{z_{mn}}\right)$。

LDA的文本生成过程中，假定话题个数$K$给定，实际通常通过实验选定。狄利克雷分布的参数$\alpha$和$\beta$通常也是事先给定。在没有其他先验知识的情况下，可以假设向量$\alpha$和$\beta$的所有分量均为1。

LDA模型整体是由观测变量和隐变量组成的联合概率分布

$$p\left(\mathbf{w},\mathbf{z},\theta,\varphi|\alpha,\beta\right)=\prod_{k=1}^K p\left(\varphi_k|\beta\right)\prod_{m=1}^M p\left(\theta_m|\alpha\right)\prod_{n=1}^{N_m}p\left(z_{mn}|\theta_m\right)p\left(w_{mn}|z_{mn},\varphi\right)$$

超参数$\alpha$和$\beta$给定条件下文本和话题的联合概率

$$p\left(\mathbf{w},\mathbf{z}|\alpha,\beta\right)=p\left(\mathbf{w}|\mathbf{z},\alpha,\beta\right)p\left(\mathbf{z}|\alpha,\beta\right)=p\left(\mathbf{w}|\mathbf{z},\beta\right)p\left(\mathbf{z}|\alpha\right)$$

由于

$$p\left(\mathbf{w}|\mathbf{z},\varphi\right)=\prod_{k=1}^K\prod_{v=1}^V\varphi_{kv}^{n_{kv}}$$

其中，$\varphi_{kv}$是第$k$个话题生成的单词集合中第$v$个单词的概率，$n_{kv}$是数据中第$k$个话题生成第$v$个单词的次数。
所以

$$\begin{align} p\left(\mathbf{w}|\mathbf{z},\beta\right) &= \int p\left(\mathbf{w}|\mathbf{z},\varphi\right) p\left(\varphi|\beta\right)\mathrm{d}\varphi \\ &= \int \prod_{k=1}^K\frac{1}{B\left(\beta\right)}\prod_{v=1}^V\varphi_{kv}^{n_{kv}+\beta_v-1}\mathrm{d}\varphi \\ &= \prod_{k=1}^K\frac{1}{B\left(\beta\right)}\int\prod_{v=1}^V\varphi_{kv}^{n_{kv}+\beta_v-1}\mathrm{d}\varphi \\ &= \prod_{k=1}^K\frac{B\left(n_k+\beta\right)}{B\left(\beta\right)} \end{align}$$

其中，$n_k=\left(n_{k1},n_{k2},\cdots,n_{kV}\right)$。

由于

$$p\left(\mathbf{z}|\theta\right)=\prod_{m=1}^M\prod_{k=1}^K\varphi_{mk}^{n_{mk}}$$

其中，$\theta_{mk}$是第$m$个文本生成的第$k$个话题的概率，$n_{mk}$是数据中第$m$个文本生成第$k$个话题的次数。
所以

$$\begin{align} p\left(\mathbf{z}|\alpha\right) &= \int p\left(\mathbf{z}|\theta\right) p\left(\theta|\alpha\right)\mathrm{d}\theta \\ &= \int \prod_{m=1}^M\frac{1}{B\left(\beta\right)}\prod_{k=1}^K\theta_{mk}^{n_{mk}+\alpha_k-1}\mathrm{d}\theta \\ &= \prod_{m=1}^M\frac{1}{B\left(\beta\right)}\int\prod_{k=1}^K\theta_{mk}^{n_{mk}+\alpha_k-1}\mathrm{d}\theta \\ &= \prod_{m=1}^M\frac{B\left(n_m+\alpha\right)}{B\left(\alpha\right)} \end{align}$$

其中，$n_m=\left(n_{m1},n_{m2},\cdots,n_{mV}\right)$。

由以上，得

$$p\left(\mathbf{w},\mathbf{z}|\alpha,\beta\right)=\prod_{k=1}^K\frac{B\left(n_k+\beta\right)}{B\left(\beta\right)} \cdot \prod_{m=1}^M\frac{B\left(n_m+\alpha\right)}{B\left(\alpha\right)}$$

由于

$$p\left(\mathbf{z}|\mathbf{w},\alpha,\beta\right)=\frac{p\left(\mathbf{w},\mathbf{z}|\alpha,\beta\right)}{p\left(\mathbf{w}|\alpha,\beta\right)}\propto p\left(\mathbf{w},\mathbf{z}|\alpha,\beta\right)$$

所以吉布斯抽样分布

$$p\left(\mathbf{z}|\mathbf{w},\alpha,\beta\right)\propto \prod_{k=1}^K\frac{B\left(n_k+\beta\right)}{B\left(\beta\right)} \cdot \prod_{m=1}^M\frac{B\left(n_m+\alpha\right)}{B\left(\alpha\right)}$$

由于$w_i$是可观测到的，所以分布$p\left(\mathbf{z}|\mathbf{w},\alpha,\beta\right)$的满条件分布

$$\begin{align} p\left(z_i|\mathbf{z}_{-i},\mathbf{w},\alpha,\beta\right) &\propto p\left(z_i,w_i|\mathbf{z}_{-i},\mathbf{w}_{-i},\alpha,\beta\right) \\ &=\iint p\left(z_i,w_i,\theta_m,\varphi_k|\mathbf{z}_{-i},\mathbf{w}_{-i},\alpha,\beta\right)\mathrm{d}\theta_m\mathrm{d}\varphi_k \\ &= \iint p\left(z_i,\theta_m|\mathbf{z}_{-i},\mathbf{w}_{-i},\beta\right) p\left(w_i,\varphi_k|\mathbf{z}_{-i},\mathbf{w}_{-i},\alpha\right)\mathrm{d}\theta_m\mathrm{d}\varphi_k \\ &= \iint p\left(z_i|\theta_m\right)p\left(\theta_m|\mathbf{z}_{-i},\mathbf{w}_{-i},\beta\right)p\left(w_i|\varphi_k\right)p\left(\varphi_k|\mathbf{z}_{-i},\mathbf{w}_{-i},\alpha\right)\mathrm{d}\theta_m\mathrm{d}\varphi_k \\ &= \int p\left(z_i|\theta_m\right) Dir\left(\theta_m|n_m+\alpha\right)\mathrm{d}\theta_m \cdot \int p\left(w_i|\varphi_k\right)Dir\left(\varphi_k|n_k+\beta\right)\mathrm{d}\varphi_k \\ &= \int \theta_{mk} Dir\left(\theta_m|n_m+\alpha\right)\mathrm{d}\theta_m \cdot \int \varphi_{kv} Dir\left(\varphi_k|n_k+\beta\right)\mathrm{d}\varphi_k \\ &= E_{Dir\left(\theta_m|n_m+\alpha\right)}\left[\theta_m\right]\cdot E_{Dir\left(\varphi_k|n_k+\beta\right)}\left[\varphi_k\right] \\ &= \frac{n_{mk}+\alpha_k}{\sum_{k=1}^K\left(n_{mk}+\alpha_k\right)}\cdot\frac{n_{kv}+\beta_v}{\sum_{v=1}^V\left(n_{kv}+\beta_v\right)} \end{align}$$

其中，$w_i$表示所有文本的单词序列的第$i$个位置的单词，是单词集合中的第$v$个单词；$z_i$表示单词$w_i$对应的话题，是话题集合中的第$k$个话题；$i=\left(m,n\right)$是二维下标，对应第$m$篇文档的第$n$个单词；$n_{mk}$表示第$m$个文本中第$k$个话题的计数，但减去当前单词的话题的计数；$n_{kv}$表示第$k$个话题中第$v$个话题的计数，但减去当前单词的话题的计数。

参数$\theta_m$的后验概率

$$\begin{align} p\left(\theta_m|\mathbf{z}_m,\alpha\right) &= \frac{p\left(\mathbf{z}_m|\theta_m\right)p\left(\theta_m|\alpha\right)}{\int p\left(\mathbf{z}_m|\theta_m\right)p\left(\theta_m|\alpha\right)\mathrm{d}\theta} \\ &=\frac{\prod_{k=1}^K\frac{1}{B\left(\alpha\right)}\theta_{mk}^{\alpha_{mk}-1}\cdot\prod_{k=1}^K\theta_{mk}^{n_{mk}}}{\int \prod_{k=1}^K\frac{1}{B\left(\alpha\right)}\theta_{mk}^{\alpha_{mk}-1}\cdot\prod_{k=1}^K\theta_{mk}^{n_{mk}}\mathrm{d}\theta} \\ &= \frac{\frac{1}{B\left(\alpha\right)}\prod_{k=1}^K\theta_{mk}^{n_{mk}+\alpha_k-1}}{\frac{1}{B\left(\alpha\right)}\int\prod_{k=1}^K\theta_{mk}^{n_{mk}+\alpha_k-1}\mathrm{d}\theta} \\ &= \frac{1}{B\left(n_m+\alpha\right)}\prod_{k=1}^K\theta_{mk}^{n_{mk}+\alpha_k-1} \\ &= Dir\left(\theta_m|n_m+\alpha\right) \end{align}$$

其中，$n_m=\left(n_{m1},n_{m2},\cdots,n_{mK}\right)$是第$m$个文本的话题的计数。

所以，参数$\theta_m$的估计

$$\theta_{mk}=E_{Dir\left(\theta_m|n_m+\alpha\right)}\left[\theta_m\right]=\frac{n_{mk}+\alpha}{\sum_{k=1}^K\left(n_{mk}+\alpha\right)}\quad m=1,2,\cdots,M;\quad k=1,2,\cdots,K$$

参数$\varphi_k$的后验概率

$$\begin{align} p\left(\varphi_k|\mathbf{w},\mathbf{z},\beta\right) &= \frac{p\left(\mathbf{w}|\mathbf{z}_k,\varphi_k\right)p\left(\varphi_k|\beta\right)}{\int p\left(\mathbf{w}|\mathbf{z}_k,\varphi_k\right)p\left(\varphi_k|\beta\right)\mathrm{d}\varphi} \\ &=\frac{\prod_{v=1}^V\frac{1}{B\left(\beta\right)}\varphi_{kv}^{\beta_{kv}-1}\cdot\prod_{v=1}^K\varphi_{kv}^{n_{kv}}}{\int \prod_{v=1}^V\frac{1}{B\left(\beta\right)}\varphi_{kv}^{\beta_{kv}-1}\cdot\prod_{v=1}^K\varphi_{kv}^{n_{kv}}\mathrm{d}\varphi} \\ &= \frac{\frac{1}{B\left(\beta\right)}\prod_{v=1}^V\varphi_{kv}^{n_{kv}+\beta_v-1}}{\frac{1}{B\left(\beta\right)}\int\prod_{v=1}^V\varphi_{kv}^{n_{kv}+\beta_v-1}\mathrm{d}\varphi} \\ &= \frac{1}{B\left(n_k+\beta\right)}\prod_{v=1}^V\varphi_{kv}^{n_{kv}+\beta_k-1} \\ &= Dir\left(\varphi_k|n_k+\beta\right) \end{align}$$

其中，$n_k=\left(n_{k1},n_{k2},\cdots,n_{kV}\right)$是第$k$个文本的话题的计数。

所以，参数$\varphi_k$的估计

$$\varphi_{kv}=E_{Dir\left(\varphi_k|n_k+\beta\right)}\left[\beta_k\right]=\frac{n_{kv}+\beta}{\sum_{v=1}^V\left(n_{kv}+\beta\right)}\quad k=1,2,\cdots,K;\quad v=1,2,\cdots,V$$

LDA吉布斯抽样算法
输入：文本的单词序列$\mathbf{w}=\left\{\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_m,\cdots,\mathbf{w}_M\right\},\mathbf{w}_m=\left(w_{m1},w_{m2},\cdots,w_{mn},\cdots,w_{mN_m}\right)$；
输出：文本的话题序列$\mathbf{z}=\left\{\mathbf{z}_1,\mathbf{z}_2,\cdots,\mathbf{z}_m,\cdots,\mathbf{z}_M\right\},\mathbf{z}_m=\left(z_{m1},z_{m2},\cdots,z_{mn},\cdots,z_{mN_m}\right)$的后验概率分布$p\left(\mathbf{z}|\mathbf{w},\alpha,\beta\right)$的样本计数，模型的参数$\varphi$和$\theta$的估计值；
参数：超参数$\alpha$和$\beta$，话题个数$K$。

1. 设所有计数矩阵的元素$n_{mk},n_{kv}$，计数向量元素$n_m,n_k$初始值为$0$；
2. 对所有文本$\mathbf{w}_m,m=1,2,\cdots,M$
   对第$m$个文本中的所有单词$w_{mn},n=1,2,\cdots,N_m$
   $\quad$抽样话题$z_{mn}=z_k\thicksim Mult\left(\frac{1}{K}\right)$；
   $\quad$增加文本-话题计数$n_{mk}=n_{mk}+1$，
   $\quad$增加文本-话题和计数$n_m=n_m+1$，
   $\quad$增加话题-单词计数$n_{kv}=n_{kv}+1$，
   $\quad$增加话题-单词和计数$n_k=n_k+1$；
3. 循环执行以下操作，知道进入燃烧期
   对所有文本$\mathbf{w}_m,m=1,2,\cdots,M$
   对第$m$个文本中的所有单词$w_{mn},n=1,2,\cdots,N_m$
   (a)当前的单词$w_{mn}$是第$v$个单词，话题指派$z_{mn}$是第$k$个话题；
   减少计数$n_{mk}=n_{mk}-1,n_m=n_m-1,n_{kv}=n_{kv}-1,n_k=n_k-1$；
   (b)按照满条件分布进行抽样 $$p\left(z_i|\mathbf{z}_{-i},\mathbf{w},\alpha,\beta\right)=\frac{n_{mk}+\alpha_k}{\sum_{k=1}^K\left(n_{mk}+\alpha_k\right)}\cdot\frac{n_{kv}+\beta_v}{\sum_{v=1}^V\left(n_{kv}+\beta_v\right)}$$ 得到新的$k^{‘}$个话题，分配给$z_{mn}$；
   (c)增加计数$n_{mk^{‘}}=n_{mk^{‘}}+1,n_m=n_m+1,n_{k^{‘}v}=n_{k^{‘}v}+1,n_{k^{‘}}=n_{k^{‘}}+1$；
   (d)得到更新的计数矩阵$N_{K\times V}=\left[n_{kv}\right]$和$N_{M\times K}=\left[n_{mk}\right]$表示后验概率分布$p\left(\mathbf{z}|\mathbf{w},\alpha,\beta\right)$的样本计数；
4. 利用得到的样本计数，计算模型参数 $$\theta_{mk}=\frac{n_{mk}+\alpha}{\sum_{k=1}^K\left(n_{mk}+\alpha\right)} \\ \varphi_{kv}=\frac{n_{kv}+\beta}{\sum_{v=1}^V\left(n_{kv}+\beta\right)}$$

变分推理基本思想：
假设模型是联合概率分布$p\left(x,z\right)$，其中$x$是观测变量，$z$是隐变量，包括参数。目标是学习模型的后验概率分布$p\left(z|x\right)$，用模型进行推理。由于后验概率是复杂分布，直接估计分布参数困难。因此用概率分布$q\left(z\right)$近似条件概率分布$p\left(z|x\right)$。其中，$q\left(z\right)$称为变分分布，相似性度量采用KL散度$D\left(q\left(z\right)||p\left(z|x\right)\right)$计算。

分布$q\left(z\right)$与分布$p\left(z|z\right)$的KL散度

$$\begin{align} D\left(q\left(z\right)||p\left(z|x\right)\right) &= \sum_z q\left(z\right)\log \frac{q\left(z\right)}{p\left(z|x\right)} \\ &= \sum_z q\left(z\right) \log q\left(z\right) - \sum_z q\left(z\right) \log p\left(z|x\right) \\ &= \sum_z q\left(z\right) \log q\left(z\right) - \sum_z q\left(z\right) \log \frac{p\left(z,x \right)}{p\left(x\right)} \\ &= \sum_z q\left(z\right) \log q\left(z\right) - \sum_z q\left(z\right) \log p\left(z,x\right) + \sum_z q\left(z\right) \log p\left(x\right) \\ &= E_q\left[\log q\left(z\right)\right] - E_q\left[\log p\left(x,z\right)\right] + \log p\left(x\right) \\ &= \log p\left(x\right) - \left\{E_q\left[\log q\left(x,z\right)\right] - E_q\left[\log p\left(z\right)\right]\right\} \end{align}$$

由于分布$q\left(z\right)$与分布$p\left(z|z\right)$的KL散度大于等于零，当且仅当两个分布一致时为零。所以，

$$\log p\left(x\right) \geq E_q\left[\log q\left(x,z\right)\right] - E_q\left[\log p\left(z\right)\right]$$

其中，不等式左端称为证据，不等式有端称为证据下界，证据下界记作

$$L\left(q\right)=E_q\left[\log q\left(x,z\right)\right] - E_q\left[\log p\left(z\right)\right]$$

在KL散度下的最优近似分布

$$\begin{align} q^*\left(z\right)&=\mathop{\arg\min}_q D\left(q\left(z\right)||p\left(z|x\right)\right) \\ &= \mathop{\arg\max}_q L\left(q\right) \end{align}$$

对变分分布$q\left(x\right)$通常假设对于$z$的所有分量都是互相独立的，即满足

$$q\left(z\right)=q\left(z_1\right)q\left(q_2\right)\cdots q\left(z_n\right)$$

这样的变分分布称为平均场。

最优近似分布是在平均场的集合，即满足独立假设的分布集合

$$Q=\left\{q\left(z\right)|q\left(z\right)=\prod_{i=1}^n q\left(z_i\right)\right\}$$

中进行的。

变分EM算法：
输入：联合概率$p\left(x,z|\theta\right)$，平均场$q\left(z\right)=\prod_{i=1}^n q\left(z_i\right)$
输出：模型参数$\theta$的估计值

1. 初始化$\theta$；
2. E步：固定$\theta$，求$L\left(q,\theta\right)$对$q$的最大化；
3. M步：固定$q$，求$L\left(q,\theta\right)$对$\theta$的最大化；
4. 得到模型参数$\theta$。

文本的单词序列$\mathbf{w}=\left(w_1,w_2,\cdots,w_n,\cdots,w_N\right)$，对应的话题序列$\mathbf{z}=\left(z_1,z_2,\cdots,z_n,\cdots,z_N\right)$，话题分布$\theta$，随机变量$\mathbf{w},\mathbf{z},\theta$的联合分布

$$p\left(\mathbf{w},\mathbf{z},\theta\right)=p\left(\theta|\alpha\right)\prod_{n=1}^N p\left(z_n|\theta\right)p\left(w_n|z_n,\varphi\right)$$

其中，$\mathbf{w}$是可观测变量，$\theta$和$\mathbf{z}$是隐变量，$\alpha$和$\varphi$是参数。

平均场变分分布

$$q\left(\theta,\mathbf{z}|\gamma,\eta\right)=q\left(\theta|\gamma\right)\prod_{n=1}^N q\left(z_n|\eta_n\right)$$

其中，$\gamma$是狄利克雷分布参数，$\eta$是多项分布参数，变量$\theta$和$\mathbf{z}$的各个分量都是条件独立的。

文本集合的证据下界

$$L\left(\gamma,\eta,\alpha,\varphi\right)=\sum_{m=1}^M\left\{E_{q_m}\left[\log p\left(\theta_m,\mathbf{z}_m,\mathbf{w}_m|\alpha,\varphi\right)\right]-E_{q_m}\left[\log q\left(\theta_m,\mathbf{z}_m|\gamma_m,\eta_m\right)\right]\right\}$$

文本$\mathbf{w}$的证据下界

$$\begin{align} L_{\mathbf{w}}\left(\gamma,\eta,\alpha,\varphi\right)&=E_q\left[\log p\left(\theta,\mathbf{z},\mathbf{w}|\alpha,\varphi\right)\right]-E_q\left[\log q\left(\theta,\mathbf{z}|\gamma,\eta\right)\right] \\ &=E_q\left[\log p\left(\theta|\alpha\right)\right]+E_q\left[\log p\left(\mathbf{z}|\theta\right)\right]+E_q\left[\log p\left(\mathbf{w}|\mathbf{z},\varphi\right)\right] \\ &\quad-E_q\left[\log q\left(\theta|\gamma\right)\right]-E_q\left[\log q\left(\mathbf{z}|\eta\right)\right] \end{align}$$

其中，$E_q\left[\cdot\right]$是对分布$q\left(\theta,\mathbf{z}|\gamma,\eta\right)$的数学期望，$\gamma$和$\eta$是变分分布的参数，$\alpha$和$\varphi$是LDA模型参数。

$$\begin{align} E_q\left[\log p\left(\theta|\alpha\right)\right]&=E_q\left[\log\frac{\Gamma\left(\sum_{l=1}^K\alpha_l\right)}{\prod_{k=1}^K\Gamma\left(\alpha_k\right)}\prod_{k=1}^K\theta_k^{\alpha_k-1}\right] \\ &= \log\Gamma\left(\sum_{l=1}^K\alpha_l\right)-\sum_{k=1}^K\log\Gamma\left(\alpha_k\right)+\sum_{k=1}^K\left(\alpha_k-1\right)E_q\left[\log\theta_k\right] \\ &=\log\Gamma\left(\sum_{l=1}^K\alpha_l\right)-\sum_{k=1}^K\log\Gamma\left(\alpha_k\right)+\sum_{k=1}^K\left(\alpha_k-1\right)\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right] \end{align}$$

其中$\theta\thicksim Dir\left(\theta|\gamma\right)$，狄利克雷分布的数学期望

$$E_{q\left(\theta|\gamma\right)}\left[\log\theta_k\right]=\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)$$

$\Psi\left(\gamma_k\right)$是对数伽马函数的导数，即

$$\Psi\left(\gamma_k\right)=\frac{\mathrm{d}}{\mathrm{d}\gamma_k}\log\Gamma\left(\gamma_k\right)$$ $$\begin{align} E_q\left(\log p\left(\mathbf{z}|\theta\right)\right)&=\sum_{n=1}^N E_q\left[\log p\left(z_n|\theta\right)\right]\\ &=\sum_{n=1}^N E_{q\left(\theta,z_n|\gamma,\eta\right)}\left[\log p\left(z_n|\theta\right)\right] \\ &=\sum_{n=1}^N \sum_{k=1}^K q\left(\theta|\gamma\right)q\left(z_n|\eta\right)\log p\left(z_n|\theta\right) \\ &=\sum_{n=1}^N \sum_{k=1}^K q\left(z_n|\eta\right) q\left(\theta|\gamma\right) \log\prod_{k=1}^K \theta_k^{n_k}\\ &=\sum_{n=1}^N \sum_{k=1}^K q\left(z_n|\eta\right) q\left(\theta|\gamma\right) \sum_{k=1}^K n_k \log\theta_k \\ &=\sum_{n=1}^N \sum_{k=1}^K q\left(z_n|\eta\right) E_{q\left(\theta|\gamma\right)}\left[\log\theta_k\right] \\ &=\sum_{n=1}^N \sum_{k=1}^K \eta_{nk}\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right] \end{align}$$

其中，$\eta_{nk}$为文档第$n$个位置的单词由第$k$个话题产生的概率。

$$\begin{align} E_q\left[\log p\left(\mathbf{w}|\mathbf{z},\varphi\right)\right]&=\sum_{n=1}^N E_q\left[\log p\left(w_n|z_n,\varphi\right)\right] \\ &=\sum_{n=1}^N E_{q\left(z_n|\eta\right)}\left[\log p\left(w_n|z_n,\varphi\right)\right] \\ &=\sum_{n=1}^N \sum_{k=1}^K q\left(z_{nk}|\eta\right)\log p\left(w_n|z_n,\varphi\right) \\ &=\sum_{n=1}^N \sum_{k=1}^K \sum_{v=1}^V \eta_{nk}w_n^v\log\varphi_{kv} \end{align}$$

其中，$w_n^v$的取值在第$n$个位置的单词是单词集合的第$v$个单词时为$1$，否则为$0$。

$$E_q\left[\log q\left(\theta|\gamma\right)\right]=\log\Gamma\left(\sum_{l=1}^K\gamma_l\right)-\sum_{k=1}^K\log\Gamma\left(\gamma_k\right)+\sum_{k=1}^K\left(\gamma_k-1\right)\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right]$$

其中，$\gamma_k$表示第$k$个话题的狄利克雷分布参数。

$$\begin{align} E_q\left[\log q\left(\mathbf{z}|\eta\right)\right]&=\sum_{n=1}^N E_q\left[\log q\left(z_n|\eta\right)\right]\\ &=\sum_{n=1}^N E_{q\left(z_n|\eta\right)}\left[\log q\left(z_n|\eta\right)\right] \\ &=\sum_{n=1}^N\sum_{k=1}^K q\left(z_{nk}|\eta\right)\log q\left(z_{nk}|\eta\right) \\ &=\sum_{n=1}^N\sum_{k=1}^K\eta_{nk}\log\eta_{nk} \end{align}$$

其中，$\eta_{nk}$表示文档第$n$个位置的单词由第$k$个话题产生的概率。

文本$\mathbf{w}$的证据下界

$$\begin{align} L_{\mathbf{w}}\left(\gamma,\eta,\alpha,\varphi\right)&=\log\Gamma\left(\sum_{l=1}^K\alpha_l\right)-\sum_{k=1}^K\log\Gamma\left(\alpha_k\right)+\sum_{k=1}^K\left(\alpha_k-1\right)\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right] \\ &+\sum_{n=1}^N \sum_{k=1}^K \eta_{nk}\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right] \\ &+\sum_{n=1}^N \sum_{k=1}^K \sum_{v=1}^V \eta_{nk}w_n^v\log\varphi_{kv} \\ &-\log\Gamma\left(\sum_{l=1}^K\gamma_l\right)+\sum_{k=1}^K\log\Gamma\left(\gamma_k\right)-\sum_{k=1}^K\left(\gamma_k-1\right)\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right] \\ &+\sum_{n=1}^N\sum_{k=1}^K\eta_{nk}\log\eta_{nk} \end{align}$$

变分参数$\eta$的估计

约束条件$\sum_{l=1}^K\eta_{nl}=1$下，证据下界关于参数$\eta$的拉格朗日函数

$$L_{\left[\eta_{nk}\right]}=\eta_{nk}\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right]+\eta_{nk}\log\varphi_{kv}-\eta_{nk}\log\eta_{nk}+\lambda_n\left(\sum_{l=1}^K\eta_{nl}-1\right)$$

其中，$\varphi_{kv}$表示（在第$n$个位置）由第$k$个话题生成第$v$个单词的概率。

对$\eta_{nk}$求偏导，得

$$\frac{\partial L}{\partial\eta_{nk}}=\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)+\log\varphi_{kv}-\log\eta_{nk}-1+\lambda_n$$

令偏导数为零，得到参数$\eta_{nk}$的估计值

$$\eta_{nk}\propto\varphi_{kv}\exp\left(\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right)$$

变分参数$\gamma$的估计

关于参数$\gamma$的证据下界函数

$$\begin{align} L_{\left[\gamma_k\right]}&=\sum_{k=1}^K\left(\alpha_k-1\right)\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right]+\sum_{n=1}^N \sum_{k=1}^K \eta_{nk}\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right] \\ &-\log\Gamma\left(\sum_{l=1}^K\gamma_l\right)+\log\Gamma\left(\gamma_k\right)-\sum_{k=1}^K\left(\gamma_k-1\right)\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right] \\ &=\sum_{k=1}^K\left[\Psi\left(\gamma_k\right)-\Psi\left(\sum_{l=1}^K\gamma_l\right)\right]\left(\alpha_k+\sum_{n=1}^N\eta_{nk}-\gamma_k\right)-\log\Gamma\left(\sum_{l=1}^K\gamma_l\right)+\log\Gamma\left(\gamma_k\right) \end{align}$$

对$\gamma_k$求偏导，得

$$\frac{\partial L}{\partial\gamma_k}=\left[\Psi^{'}\left(\gamma_k\right)-\Psi^{'}\left(\sum_{l=1}^K\gamma_l\right)\right]\left(\alpha_k+\sum_{n=1}^N\eta_{nk}-\gamma_k\right)$$

令偏导数为零，得到参数$\eta_k$的估计值

$$\gamma_k=\alpha_k+\sum_{n=1}^N\eta_{nk}$$

LDA的变分参数估计算法：

1. 初始化：对所有$k$和$n$，$\eta_{nk}^{\left(0\right)}=1/K$
2. 初始化：对所有$k$，$\gamma_k=\alpha_k+N/K$
3. 重复
   $\quad$对$n=1$到$N$
   $\quad\quad$对$k=1$到$K$
   $\quad\quad\quad n_{nk}^{\left(t+1\right)}=\varphi_{kv}\exp\left[\Psi\left(\gamma_k^{\left(t\right)}\right)-\Psi\left(\sum_{l=1}^K\gamma_l^{\left(t\right)}\right)\right]$
   $\quad\quad$规范化$\eta_{nk}^{\left(t+1\right)}$使其和为$1$
   $\quad\gamma^{\left(t+1\right)}=\alpha+\sum_{n=1}^N\eta_n^{\left(t+1\right)}$
   直到收敛

给定一个文本集合$D=\left\{\mathbf{w}_1,\cdots,\mathbf{w}_m,\cdots,\mathbf{w}_M\right\}$，模型参数$\alpha$和$\varphi$的估计是对所有文本同时进行。

模型参数$\varphi$的估计

在约束条件$\sum_{v=1}^V=1,k=1,2,\cdots,K$下，证据下界关于参数$\varphi$的拉格朗日函数

$$L_{\left[\varphi_{kv}\right]}=\sum_{m=1}^M \sum_{n=1}^{N_m} \sum_{k=1}^K \sum_{v=1}^V \eta_{mnk}w_{mn}^v\log\varphi_{kv}+\sum_{k=1}^K\lambda_k\left(\sum_v=1^V\phi_{kv}-1\right)$$

对$\varphi_{kv}$求偏导并令其为零，归一化求解，得到参数$\varphi_{kv}$的估计值

$$\varphi_{kv}=\sum_{m=1}^M\sum_{n=1}^{N_m}\eta_{mnk}w_{mn}^v$$

其中，$\eta_{mnk}$为第$m$个文本的第$n$个单词属于第$k$个话题的概率，$w_{mn}^v$在第$m$个文本的第$n$个单词是单词集合的第$v$个单词时取值为$1$，否则为$0$。

模型参数$\alpha$的估计

关于参数$\alpha$的证据下界函数

$$L_{\left[\alpha_k\right]}=\sum_{m=1}^M\left\{\log\Gamma\left(\sum_{l=1}^K\alpha_l\right)-\sum_{k=1}^K\log\Gamma\left(\alpha_k\right)+\sum_{k=1}^K\left(\alpha_k-1\right)\left[\Psi\left(\gamma_{mk}\right)-\Psi\left(\sum_{l=1}^K\gamma_{ml}\right)\right]\right\}$$

对$\alpha_k$求偏导，得

$$\frac{\partial L}{\partial\alpha_k}=M\left[\Psi\left(\sum_{l=1}^K\alpha_l\right)-\Psi\left(\alpha_k\right)\right]+\sum_{m=1}^M\left[\Psi\left(\gamma_{mk}\right)-\Psi\left(\sum_{l=1}^K\gamma_{ml}\right)\right]$$

再对$\alpha_l$求偏导，得

$$\frac{\partial^2 L}{\partial\alpha_k\partial\alpha_l}=M\left[\Psi^{'}\left(\sum_{l=1}^K\alpha_l\right)-\delta\left(k,l\right)\Psi^{'}\left(\alpha_k\right)\right]$$

其中，$\delta\left(k,l\right)$是delta函数。

应用牛顿法，用以下公式迭代

$$\alpha_{new}=\alpha_{old}-H\left(\alpha_{old}\right)^{-1}g\left(\alpha_{old}\right)$$

其中，$g\left(\alpha\right)$是变量$\alpha$的梯度，$H\left(\alpha\right)$是变量$\alpha$的Hessian矩阵。得到参数$\alpha$的估计值。

LDA的变分EM算法：
输入：给定文本集合$D=\left\{\mathbf{w}_1,\cdots,\mathbf{w}_m,\cdots,\mathbf{w}_M\right\}$
输出：变分参数$\gamma,\eta$，模型参数$\alpha,\varphi$
交替执行E步和M步，直到收敛

1. E步
   固定模型参数$\alpha,\varphi$，通过关于变分参数$\gamma,\eta$的证据下界最大化，估计变分参数$\gamma,\eta$。
2. M步
   固定变分参数$\gamma,\eta$，通过关于模型参数$\alpha,\varphi$的证据下界最大化，估计模型参数$\alpha,\varphi$。

根据变分参数$\left(\gamma,\eta\right)$，可以估计模型参数$\theta=\left(\theta_1,\cdots,\theta_m,\cdots,\theta_M\right),\mathbf{z}=\left(z_1,\cdots,z_m,\cdots,z_M\right)$。